wald检验百度百科_wald检验统计量

2024-09-15 04:30:36

1.Likelihood Ratio, Wald和Lagrange Multiplier(Score)检验的区别与相似点

2.高级计量经济学 13：最大似然估计(下)

3.wald检验的原设是什么呢

4.eviews5.0下wald检验的结果怎么看啊

wald检验百度百科_wald检验统计量

Wald Test:

Equation: EQ01

Test Statistic Value df Probability

F-statistic 10.38003 (1, 10) 0.0091

Chi-square 10.38003 1 0.0013

Null Hypothesis Summary:

Normalized Restriction (= 0) Value Std. Err.

C(1) - 0.5*C(2) -1.4281 61.27872

Restrictions are linear in coefficients.

如上图所示例子，检测C(1) - 0.5*C(2)是否等于0（约束条件），主要看Chi-square后面的P值，在此例子中，P为0.0013<0.005所以拒绝原设，即原设不成立，回归方程在约束条件下不成立或者不显著。

Likelihood Ratio, Wald和Lagrange Multiplier(Score)检验的区别与相似点

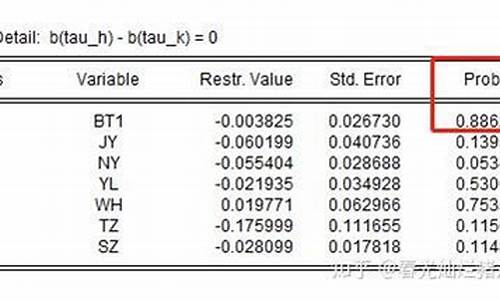
就是说这些参数都相等。第一幅图原设是C2=C3，然后3个检验测试结果的p值都远远大于0.05，那么无法否定原设，认为C2=C3. 下面的都同理，你的p值都在0.5附近，大得很。每幅图的第二个表是告诉你均值和标准差的，如此可以算95%置信区间。

高级计量经济学 13：最大似然估计(下)

本文是对参考原文链接这篇文章的翻译。如有疑问或译文有误，可留言修正。

本文尝试这些基本概念1)似然比检验2)Wald检验3)分数检验。

一位研究员想要估计下面这个模型，该模型使用 gender ， read ， math , science 四个预测变量预测学生在标准测试中的 High vs low writing score 。模型结果如图1.

现在研究员想知道，图1中的模型(使用4个预测变量)会不会比只使用两个预测变量（ gender , read )时的模型更显著。研究员将如何进行这种比较呢? 有三种常用检验可以用来检验这类问题，他们是似然比检验LR ， Wald检验和拉格朗日乘子检验(有时也叫分数检验) 。这些设检验有时被描述成检验嵌套子模型区别的的检验，因为模型中的一个了可以理解成被内嵌在另一个模型中。就像两个预测变量的模型其实可理解成是四个预测变量的子模型，那么想要知道嵌套子模型与全变量模型的好坏区别就可以使用上述的三种检验去做评估。

上述三种检验都通过比较模型的似然值来评估他们的拟合度。似然是一个概率，表达的是已知某种结果对应某个参数估计值的概率(具体理解见图2)。模型的目标是找到一个参数值（系数）使得似然函数值最大，也就是说找到一组参数可以最大程度的近似数据集。很多应用程序使用对数似然函数，而不是似然函数，这是因为对数似然函数计算起来更方便。对数似然函数永远是负数，值越大（越接近于0）表明拟合模型更好。尽管上面图1中的模型是逻辑回归，但这些检验方法非常通用，可以应用于具有似然函数的任何模型。

上面已经提到过，似然函数是参数与数据的函数。当数据集一旦确定就不再改变，可以改变系数估计值使得似然函数达到最大值。不同的参数值，或者估计值的集合将对应不同的似然概率。如图3所示，图中曲线体现出对数似然值随着参数a的变化而变化的趋势。X轴是参数a的值，Y轴是参数a取某值时对应的似然函数值。大多数模型都多个参数但如果模型中的其他参数固定不变，改变其中一个参数如a时就会呈现出图3中的相似的曲线。垂直的这条线标记出最大似然值对应的a的取值。

似然比检验（以后简写为LR)被用来评估两个模型并且比较两个模型的拟合效果。从一个模型中删除掉几个预测变量往往会使模型拟合效果变差（比如，会得到一个更小的对数似然概率），但这对于检验所观察的模型拟合度是否具有统计显著性来说是必要的。 LR通过这种方式来比较两个模型的对数似然值来检验两个模型，如果此差异（两个模型的对数似然值差异）是统计显著的，那么限制性更小的模型（参数更多的模型）相对限制性更大的模型对数据的拟合更好。如果你已经有了一个模型的对数似然值，那么LR检验值就很容易计算了。LR检验统计值计算公式如下：

其中指对应模型的似然函数值，表示模型的自然对数似然函数值。指系数少的模型，表示系数更多的模型。

检验统计结果服从卡方分布，自由度等于受约束的参数个数，比如这里相对全变量模型，只有2个参数的模型少了两个变量，所以自由度为2，所以检验统计结果服从自由度为2的卡方分布。

使用上面的两个模型，使用LR检验他们的差异。模型1是只使用两个 gender 和 read 两个变量的模型（没有 math 和 science ,我们将它们的系数限制为0），图4是模型1的结果，结果中标记出了对数似然函数值（我们不对模型结果进行解释，这不是文章的目的）。

现在再运行模型2，模型2中使用4个预测变量，图5是模型结果。同样我们仅标记出模型2的对数似然值，并不对模型的做过多的解释。

既然有了两个模型的对数似然值，我们可以计算LR。代入公式我们有

即我们的似然比是36.05（服从自由度为2的卡方分布）。我们现在可使用一张表或者其它手段得知36.05对应的 , 这表示全变量模型相对两个变量的子模型拟合数据更显著。值得注意的是，很多统计工具包会都会计算两个模型的LR检验去比较两个模型，我们现在手动做是因为它计算简单且可以更好的帮助理解似然比检验的工作原理。

Wald与LR相似，但比LR要简单，因为它只需要评估一个模型。Wald通过检验的工作原理是检验一组参数等于某个值的零设。对被检测的模型来说，零设是指感兴趣的两个系数是否同时为零。如果检验结果无法拒绝零设，表明移除这两个变量将不会严重影响模型对数据的拟合效果，因为相对系数标准差很小的系数通常对因变量的预测没有太大帮助。Wald的计算公式相对LR来说有点繁琐所以这里不会列出，可参考（Fox, 19, p569）。为了让大家直观的感受Wald如何工作，它会测试标准误差下估计参数距离0有多远（或者是零设下的其他值），wald的结果和其他回归结果的设检验很类似。只不过wald可以同时检验多个参数，而经典的做法是在回归结果中一次只检验一个参数。图6显示了四个变量的模型，也不是模型2的结果。

图7中第一部分列出了wald检验的零设，即 math和science对应的系数同时为0 。第二部分列出了模型2执行wald检验后的卡方分布值为27.53，其对应的自由度为2的卡方分布的 p_value=0.0000 ，即p值掉入拒绝域，我们可以拒绝两个参数同时为0的设。因为包括具有统计意义的预测变量应该会导致更好的预测（即更好的模型拟合），所以我们可以得出结论，包括 math 和 science 变量会使模型拟合的统计得到显著改善。

与Wald检验一样，Lagrange乘数检验仅需要估计一个模型。区别在于，使用拉格朗日乘数检验时，估计的模型不包含感兴趣的参数。这意味着，在我们的示例中，我们可以使用拉格朗日乘数检验来测试在仅使用 gender 并将其作为预测变量运行的模型之后，向模型中添加 science 和 math 是否会导致模型拟合度显著改善。基于在模型中变量（ female 和 read ）的观察值处的似然函数的斜率来计算测试统计量。该估计的斜率或“分数”是拉格朗日乘数测试有时称为得分测试的原因。如果在模型中包括其他变量，则将分数用于估计模型拟合的改进。如果将变量或变量集添加到模型，则测试统计量是模型卡方统计量的预期变化。因为如果将当前遗漏的变量添加到模型中，它会测试模型拟合的改进，所以拉格朗日乘数检验有时也称为遗漏变量的检验。它们有时也称为修改索引，尤其是在结构方程建模文献中。图8是使用变量female和作为hiwrite的预测变量读取的逻辑回归模型的输出（与LR测试的模型1相同）。

运行上述模型后，我们可以查看拉格朗日乘数测试的结果。与前两个测试不同，前两个测试主要用于在向模型中添加多个变量时评估模型拟合的变化，而拉格朗日乘数测试可以用于测试模型拟合的预期变化（如果一个或多个参数为当前受限的被允许自由估计。在我们的示例中，这意味着测试向模型添加 math和science 是否会显着改善模型拟合。图10是分数测试的输出。表中的前两行提供了将单个变量添加到模型的测试统计信息（或分数）。为了继续我们的示例，我们将重点关注第三行中标记为“同时测试”的结果，该结果显示了在模型中同时添加数学和科学的测试统计量。将数学和科学都添加到模型的测试统计量为35.51，它是卡方分布的，自由度等于要添加到模型中的变量的数量，因此在我们的示例中为2。p值低于典型的截止值0.05，表明在模型中包含数学和科学变量将在模型拟合方面产生统计学上的显着改善。该结论与LR和Wald检验的结果一致。

如上所述，这三个测试都解决了相同的基本问题，即是否将参数约束为零（即忽略这些预测变量）会降低模型的拟合度？它们的区别在于他们如何回答该问题。如您所见，为了执行似然比检验，必须估计一个人希望比较的两个模型。 Wald和Lagrange乘数（或分数）检验的优势在于，它们近似于LR检验，但只需要估计一个模型即可。 Wald和Lagrange乘数检验在渐近上都等同于LR检验，也就是说，随着样本量变得无限大，Wald和Lagrange乘数检验统计的值将越来越接近LR检验的检验统计量。在有限的样本中，这三个样本往往会产生不同的检验统计量，但通常得出相同的结论。三种检验之间的有趣关系是，当模型为线性时，三种检验统计量具有以下关系Wald≥LR≥评分（Johnston和DiNardo 19，第150页）。也就是说，Wald检验统计量将始终大于LR检验统计量，而LR检验统计量将始终大于分数测试中的检验统计量。当计算能力受到更大限制，并且许多模型需要很长时间才能运行时，能够使用单个模型来近似LR测试是一个相当大的优势。如今，对于大多数研究人员可能想要比较的模型而言，计算时间已不再是问题，我们通常建议在大多数情况下运行似然比检验。这并不是说永远不要使用Wald或成绩测试。例如，Wald检验通常用于对用于建模回归中的预测变量的虚拟变量集执行多自由度测试（有关更多信息，请参阅我们的《关于Stata，SPSS和SAS回归的网络手册》，特别是第3章–使用分类预测变量进行回归。）分数测试的优势在于，当候选变量数量很大时，它可用于搜索省略的变量。

更好地了解这三个测试之间如何关联以及它们如何不同的一种方法是查看它们所测试内容的图形表示。上图说明了这三个测试的每一个。沿x轴（标记为“ a”）是参数a的可能值（在我们的示例中，这是数学或科学的回归系数）。沿y轴是与a的那些值相对应的对数似然值。 LR测试将模型的对数似然率与参数a的值（被限制为某个值（在我们的示例中为零））与自由估计a的模型进行比较。它通过比较两个模型的可能性高度来查看差异是否在统计上显着（请记住，可能性值越高表示拟合越好）。在上图中，这对应于两条虚线之间的垂直距离。相反，Wald测试将参数估计值a-hat与a_0进行比较； a_0是零设下a的值，通常设a =0。如果a-hat与a_0明显不同，则表明自由估计a（使用a-hat）可显着改善模型拟合。在图中，这表示为x轴上a_0和a-hat之间的距离（由实线突出显示）。最后，当a受到约束（在我们的示例中为零）时，得分测试着眼于对数似然率的斜率。也就是说，它查看了在（零）设的a值处改变可能性的速度。在上图中，这显示为a_0处的切线。

wald检验的原设是什么呢

此文内容为《高级计量经济学及STATA应用》的笔记，陈强老师著，高等教育出版社出版。

我只将个人会用到的知识作了笔记，并对教材较难理解的部分做了进一步阐述。为了更易于理解，我还对教材上的一些部分（ 包括证明和正文 ）做了修改。

在计量经济学中，常常使用以下三类大样本下渐近等价的统计检验。对于 线性回归模型 ，检验原设为，其中为未知参数，已知，共有个约束。

通过研究的无约束估计量和的距离来进行检验

他检验的东西是我所估计出来的是否可能等于

其基本思想是，如果正确，那么与的距离应该不要很大（注意，这里是和的距离）。Wald Test 统计量为：

其中，为约束条件的个数（即解释变量的个数），其证明在高级计量第6、7期有，大家可以回顾（也可以在我的上看）， 我在这里多嘴说一下如何理解它 。

我们从标量的情形开始。显然衡量了和的距离。但是，这有两个问题：

由于出现了上面的两个困境，于是我们就很容易想到标量情形下 Wald Test 的表达式：

也就是：

的形式。

很容易拓展到向量的情形。如果我们要对多个参加进行检验，那么就变成了向量，此时虽然也可以反映两个向量之间的距离，但绝对值的数学性质并不良好，我们更多的是使用欧拉距离，也就是使用

的形式（ 二次型 ）。同样地，这个式子还没有解决把握和量纲的问题，于是我们也需要对它除以“标准差”。我们前面已经反复强调，在向量下的除法运算就是逆、向量下的方差就是 协方差矩阵 、向量下的二次函数就是 二次型 ，那么于是我们就有：

这就是 Wald Test 统计量的来源。至于它如何收敛到分布，请移步高级计量第6、7期。

通常来说，无约束的似然函数最大值比有约束的似然函数最大值更大，这是因为无约束条件下的参数空间显然比带约束的参数空间更大，即：。

LR的思想是，如果正确，那么不应该很大。在正确下，，那么LR统计量就是：

证明的方法是将LLF做二阶泰勒展开（因为MLE的一阶条件表明，，可以看前一篇文章）。高级计量7 中的统计的似然比表达式就是按照这个原理设计的。

下面的证明我没有参考别的资料，我尽量做到严谨，推着玩玩儿。

考虑有约束条件的对数似然函数最大化问题：

引入拉格朗日函数：

其中，为拉格朗日乘子向量，如果，那么说明此约束条件不紧（tight）或者不是 硬约束 （binding constraint），加上这个约束条件并不会使似然函数的最大值下降很多，即原设很可能成立。根据上述问题的一阶条件，对求导，有：

即最优的拉格朗日乘子等于似然函数在处的梯度向量，那么统计量为：

其中，为信息矩阵在处的取值。由于有被称作 得分函数 （score function），所以这个检验也被称为得分检验（score test）；而正正是得分函数的协方差矩阵，这我们前面已经证明过了。直观来说，就是由于在无约束估计量处，得分函数为向量，那么如果原设成立，那么在约束估计量处，梯度向量也应该接近于向量，即：

而统计量反应的就是此接近程度。

总之，Wald检验仅利用无约束估计的信息；LM检验仅使用有约束估计的信息；LR检验同时利用了有约束和无约束估计的信息。在原设为下，我总结了下表：

在大样本下，三种检验是渐近等价的；在小样本下，。

另外，如果不对模型的具体概率分布作设，则无法得到似然函数，于是就一般没有办法使用检验和检验；不过检验依然可以使用。所以检验的使用范围最广。

如果随机变量不服从正态分布，却使用了以正态分布为前提的最大似然估计法，该估计量 仍有可能是一致的 ！

定义使用不正确的似然函数而得到的最大似然估计，称为准最大似然估计（Quasi MLE, QMLE）或伪最大似然估计（Pseudo MLE）。

之所以在某些情况下可以“歪打正着”地得到一致估计的准最大似然估计，是因为 MLE 也可以被视为 GMM，而后者并不需要对随机变量的具体分布作出定（见教材第10章）。也就是说，虽然 MLE 要求随机变量服从正态分布，不过这个定其实可以稍微放松。如果 QMLE 满足以下条件，那么它依然是一致估计量：

然而，更一般的情况下， QMLE 并非一致估计 ，比如 14 章的 Tobit 回归。就算 QMLE 恰巧为一致估计，但其渐近方差也通常不是一致估计（即参数估得准，不过参数的不确定性估不准）。

设正确的对数似然函数为而被误设为，那么我们称后者为准对数似然函数（pseudo log likelihood function, PLLF）。最大化的结果也就是 QMLE 估计量：

类似于 MLE 一致性的证明步骤，我们可以证明，其中称为准真实值（peseudo-true value），但通常。对于的大样本分布，可以用类似于 MLE 的推导证明：

其中，和的表达式类似于和的表达式。不过，由于并非真实的 LLF，所以信息矩阵等式不再成立，于是通常，这为渐近正态的协方差矩阵的进一步简化造成了麻烦。

在我们 很有把握 的条件下，我们可以用基于的标准误差来设检验，这被称为胡贝尔-怀特稳健标准误（Huber-White robust standard errors）。这个标准误也被称为稳健标准误，因为它与第 5 章介绍的 异方差稳健标准误 是一致的。需要注意的是，如果，就算使用稳健的标准误也 无济于事 ，你首先要考虑的是估计的一致性问题。

对线性回归模型，如果扰动项不服从正态分布，则虽然OLS 估计量是一致的且服从正态分布，但是无法使用小样本 OLS 进行设检验。在这种情形下，就需要对扰动项是否服从正态分布进行检验。当然，如果是大样本，那就可以用渐近正态的理论处理，我们也不关心扰动项是否服从正态分布了。

不过，对非线性模型使用 MLE 时，由于正态分布定时推导 MLE 的前提，故而检验扰动项是否服从正态分布可能就显得比较重要。

为了考察扰动是否正态，最直观的方法是画图。可以把残差画成直方图，然后用核密度估计方法得到光滑的曲线，然后与正态分布的曲线进行对比。一个核密度估计的例子如下图所示：

eviews5.0下wald检验的结果怎么看啊

wald检验的原设是：线性约束成立。

沃尔德检验亦称序贯概率比检验、序贯似然比检验。以似然比做统计量的序贯检验。

沃尔德检验是数理统计学的一个分支，其名称源出于亚伯拉罕·瓦尔德在1947年发表的一本同名著作，它研究的对象是所谓“序贯抽样方案”，及如何用这种抽样方案得到的样本去作统计推断。

序贯抽样方案是指在抽样时，不事先规定总的抽样个数（观测或实验次数）,而是先抽少量样本,根据其结果，再决定停止抽样或继续抽样、抽多少，这样下去，直至决定停止抽样为止。反之，事先确定抽样个数的那种抽样方案，称为固定抽样方案。

提出者背景：

亚伯拉罕·瓦尔德（Abraham Wald,1902～1950），罗马尼亚裔美国统计学家，1902年10月31日生于罗马尼亚克卢日的一个正统犹太世家，由于宗教信仰的因素，他受教育的机会受到某些限制，而必须靠自修弥补。

他的自修取得了极大成效，使他能对希尔伯特 (Hilbert) 的《Foundation of Geometry》提出有价值的见解，并被列入该书的第七版中。这一事实充分显示了他的数学天赋。

序贯分析是数理统计学的一个分支。其名称源出于美国统计学家瓦尔德在1947年发表的一本同名著作。在研究决策问题时，不是预先固定样本量（观察数目），而是逐次取样（观察），直到样本提供足够的信息，能恰当地作出决策为止。这样的统计决策过程称为序贯分析。